WebGL入门教程6 - 光照效果和Phong光照模型
正是因为有了光,世界才能被我们看见,在3D的世界里,光照给物体带来真实的视觉感受。
当光照射在某一表面上时,它可能被吸收、反射或投射。其中入射到表面上的一部分光能被吸收并转化为热,其余部分被反射或投射。正是反射和透射使得物体可见。如果入射光全部被吸收,物体将不可见,该物体称为黑体。光能中被吸收、反射或透射的数量决定于光的波长。若入射光中所有波长的光被吸收的量近似相等,则在白光(包含所有波长的光)的照射下,物体呈现灰色,如果只有少数被吸收,则物体呈现白色。如果是红色光源照射在绿色物体(即吸收除绿色之外的光,反射绿色光),由于红色光被吸收,物体也呈现黑色。
从物体表面反射或透射出来的光取决于光源中的光的成分、光线的方向、光源的几何形状以及物体表面的朝向和表面性质等。物体表面的反射光又可分为漫反射光、镜面反射光和透射光。漫反射光和透射光可以认为是光穿过物体表面并被吸收,然后重新发射出来的光。漫反射光均匀的散布在各个方向,因此观察者的位置是无关紧要的。而镜面反射光则由物体的外表面直接反射而成,它并不穿透物体表面,不会出现散射,和光线入射角度和观察者的位置有关,很直观的靠近反射光束方向的角度,更容易受镜面反射光的影响,想一想小时候用镜子反射太阳光晃小伙伴眼睛的小恶作剧,很容易明白这个道理。
通常,物体表面的材料是绝缘体或导体。绝缘材料是透明的,导体是不透明的。透明材料反射线很弱,而不透明材料的反射性很强。
对于漫反射光,计算机图形学建立了一个简单的光照模型:
I = Ia*ka + (Il*kd*cosθ)/(dp+K) (0<=p<=2)
其中Ia*ka是环境光(泛光源)分量,(Il*kd*cosθ)/(dp+K)是漫反射光分量,漫反射光强度和入射光线与物体表面法线之间夹角(θ)的余弦成正比,并和物体与观察点的距离(d)成反比。
而对于镜面反射光,计算模型如下:
I(λ)s = Il(λ)w(i,λ)cosna
其中w(i,λ)是反射率曲线,它给出了镜面反射光线和入射光线的比例,是入射角i和光波长λ的函数。n为幂次,用于模拟反射光的空间分布。
n越大,反射光线越集束,反之则越是扩散。a是反射光线和视线之间的夹角,显然角度越大,视觉影响越小。
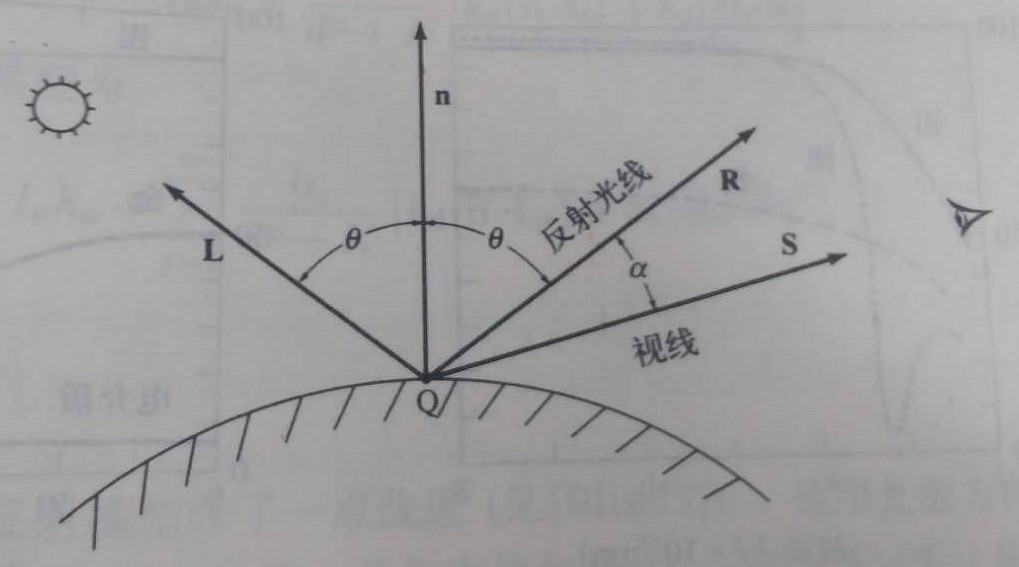
将泛光照射(环境光,代表随机分布光源)、漫反射和镜面反射结合在一起就得到了WebGL中实际常用的Phong光照模型。

上图来自WIKI,很形象的说明了Phong反射模型合成原理,其中Ambient是泛光、Diffuse是漫反射、Specular是镜面反射。
(注:Phong是一名越南籍计算机科学家的名,该科学家姓Bui。全名Bui Tuong Phong,我倾向于翻译为毕桐风,网上的“冯氏”翻译是明显错误的。这不影响理论本身,但正确的命名可以避免沟通误差。)
在本文中,我们将沿用教程5中的立方体,来演示如何在WebGL中运用光照模型。
为了简化起见,我们把立方体看成是导体(不透明),并将只考虑漫反射和环境光,而忽略镜面反射。
我们将使用纹理的颜色来计算漫反射和环境光,并只会考虑一种最简单的漫反射光,那就是平行光。
所谓平行光源,指的是当光源离物体距离很远时,光束几乎是平行照射在物体表面:

典型的如太阳光,我们就可以把它当作是平行光。除此之外还有点光源,比如家中的电灯泡:
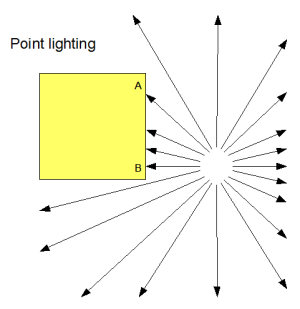
对于点光源,每个顶点的入射方向都需要独立计算,这使得光照效果的计算变得较为复杂。这里我们暂不考虑。
对于平行光源,每个顶点的入射方向都是相同的,因此可以使用一个uniform变量来表示。
除了入射方向之外,我们还需要知道物体表面的方向,这可以通过表面法向量来表示。这样根据前面的计算公式,就能得到漫反射分量。
在WebGL中,步骤如下:
在3D建模时,确定并保存每个顶点的法线向量(normal vector)
指定光线方向向量(light vector)
在顶点着色器中计算法线向量和光线方向向量的点积,然后计算出相应的颜色值,同时加入环境光的分量
在3D立方体贴图的程序中,initBuffer函数用来建立顶点数据,现在我们需要添加法向量数据计算逻辑:
cubeVertexNormalBuffer = gl.createBuffer(); gl.bindBuffer(gl.ARRAY_BUFFER, cubeVertexNormalBuffer); var vertexNormals = [ // 前面 0.0, 0.0, 1.0, 0.0, 0.0, 1.0, 0.0, 0.0, 1.0, 0.0, 0.0, 1.0, // 后面 0.0, 0.0, -1.0, 0.0, 0.0, -1.0, 0.0, 0.0, -1.0, 0.0, 0.0, -1.0, // 上面 0.0, 1.0, 0.0, 0.0, 1.0, 0.0, 0.0, 1.0, 0.0, 0.0, 1.0, 0.0, // 下面 0.0, -1.0, 0.0, 0.0, -1.0, 0.0, 0.0, -1.0, 0.0, 0.0, -1.0, 0.0, // 右侧 1.0, 0.0, 0.0, 1.0, 0.0, 0.0, 1.0, 0.0, 0.0, 1.0, 0.0, 0.0, // 左侧 -1.0, 0.0, 0.0, -1.0, 0.0, 0.0, -1.0, 0.0, 0.0, -1.0, 0.0, 0.0, ]; gl.bufferData(gl.ARRAY_BUFFER, new Float32Array(vertexNormals), gl.STATIC_DRAW); cubeVertexNormalBuffer.itemSize = 3; cubeVertexNormalBuffer.numItems = 24;
然后在drawScene绘制函数中,绑定缓存到相应的着色器属性(attribute):
gl.bindBuffer(gl.ARRAY_BUFFER, cubeVertexNormalBuffer); gl.vertexAttribPointer(shaderProgram.vertexNormalAttribute, cubeVertexNormalBuffer.itemSize, gl.FLOAT, false, 0, 0);
然后我们来创建相关光源:
//白色环境光 gl.uniform3f( shaderProgram.ambientColorUniform, 1.0,//RGB中的RED分量 1.0,//RGB中的GREEN分量 1.0 //RGB中的BLUE分量 ); var lightingDirection = [1.0, -1.0, 1.0]; //模拟上午的太阳光,靠近视点的面会显得偏暗 var adjustedLD = vec3.create(); vec3.normalize(lightingDirection, adjustedLD); vec3.scale(adjustedLD, -1); gl.uniform3fv(shaderProgram.lightingDirectionUniform, adjustedLD); //白色平行光源 gl.uniform3f( shaderProgram.directionalColorUniform, 1.0,//RGB中的RED分量 1.0,//RGB中的GREEN分量 1.0 //RGB中的BLUE分量 );
上面的代码中vec3.normalize用来把lightingDirection变成单位向量,差不多是(0.577,-0.577,0.577)。
然后vec3.scale用来把光线入射坐标换成光线方向(倒置一下,比如去向是西边,应来自东边。)
这样我们有了物体模型的顶点法向量数据和光源后,我们就可以按Phong模型来计算光照效果了。
在此之前我们还需要把顶点法向量数据做一个转换,如同顶点数据所做的mvp(model/view/projection)转换类似,
但是和顶点不同的是,法向量需要始终保持“单位”向量的属性,不能出现长短变化和因此而导致的方向偏离,
我们使用下面的变换矩阵:
var normalMatrix = mat3.create(); mat4.toInverseMat3(mvMatrix, normalMatrix); mat3.transpose(normalMatrix); gl.uniformMatrix3fv(shaderProgram.nMatrixUniform, false, normalMatrix);
前面2行把法向量矩阵的top/left开始的3*3矩阵求其逆矩阵,第3行求其转置矩阵(行列交换)。
最后1行把着色器程序的nMatrixUniform变量设置为变换后的法向量矩阵。
为什么要先求逆然后再求转置,这是根据平面法向量和顶点之间的切线无论在转换前还是转换后都保持正交这样一个基本特征推导出来的计算公式。这里不做过多说明,以后或会单独发文详细说明公式的推导过程,我们这里还是先重点关注整体的光照处理过程。
(注:3D空间坐标只要vec3就可以表示,为什么出现vec4这样的数据结构呢?这是为了区分矢量和坐标,引入了第4维数据,当为0时表示为矢量(比如上面的法向量),非0时,表示空间坐标。在矩阵变换中第4维的数可以用来实现平移变换。)
接下来我们处理着色器程序,实现Phong计算模型,下面是顶点着色器的代码:
vec3 transformedNormal = uNMatrix * aVertexNormal; float directionalLightWeighting = max(dot(transformedNormal, uLightingDirection), 0.0); vLightWeighting = uAmbientColor + uDirectionalColor * directionalLightWeighting;
最后我们在片段着色器中,把顶点RGB颜色乘上光照系数就完成了整个光照效果的绘制:
vec4 textureColor = texture2D(uSampler, vec2(vTextureCoord.s, vTextureCoord.t)); gl_FragColor = vec4(textureColor.rgb * vLightWeighting, textureColor.a);
你可以自己在线试试看(含完整源代码)。
 21899
21899
 0
0
最新评论
- 相关文章
CentOS6 Apache2.2多站点HTTPS配置
可以使用letsencrypt(certbot)免费证书服务。支持多系统、多站点和多目录,支持wildcard(通配符域名),90天生效,可用定时任务自动更新。需要注意一点的是apache2.4以下版本需要在默认的ssl配置中添加如下的指令:NameVirtualHost
3D感知和建模关键硬件技术:双目、3D结构光和TOF
无论VR、AR和3D打印,其核心技术包含3D成像和建模。而3D建模属于劳动密集型的工作,耗时耗力,凡这类工作都会是被新技术革命的地方,自动3D建模技术就是为了解决...
常见面试题JS语言中四种函数调用方式实例讲解
JS的语言世界中函数(function)是一等公民,函数的调用有多种方法。普通调用这个是最常见和直接的方式:function
深入理解JS和CSS3动画性能问题和技术选择
本文对比了JS及其框架和CSS3的动画性能,并深入剖析了其内在原因。技术结论大致如下:1. jQuery出于设计原因,在动画性能上表现最差2. CSS3由于把动画逻辑推给了...
通过实例深入理解HTML5/CSS3/SVG/WebGL的技术本质
使用HTML5 FileReader和Canvas压缩用户上传的图片
手机用户拍的照片通常会有2M以上,这对服务器带宽产生较大压力。因此在某些应用下(对图片要求不那么高)我们可以在客户端来压缩图片,然后再提交给服务器。总体...
计算WebGL中的uniforms变量使用数
在使用Three.js为人体模型加载皮肤材料时,启用了skinning:true的参数。有时候会导致GL编译错误,提示“too many uniforms”。下面的文章有助于理解错误原因和检...
深入理解Three.js(WebGL)贴图(纹理映射)和UV映射
本文将详细描述如何使用Three.js给3D对象添加贴图(Texture Map,也译作纹理映射,“贴图”的翻译要更直观,而“纹理映射”更准确。)。为了能够查看在线演示效...
Three.js入门教程4 - 创建粒子系统动画
嗨,又见面了。这么说我们已经开始学习Three.js了,如果你还没有看过之前三篇教程,建议你先读完。如果你已经读完前面的教程了,你可能会想做一些关于粒子的东西。让我们直面这个话题吧,每个人都爱粒子效果。不管你是否知道,你可以很轻易地创建它们。
WebGL入门教程5 - 详解纹理滤镜(Texture Filter)
WebGL中使用纹理贴图来实现细腻的物体表面观感,其中一个重要的参数是纹理滤镜(Texture Filter)。
这个参数用来处理当对象出现缩放时,纹理如何处理中间...如何使用WebGL实现空气高温热变形动画特效
我们在炎炎夏日,或者在火堆旁,经常会观察到热源周围空气的不稳定波动现象。本文将讲解如何通过WebGL来实现这个特效。该效果可用于热变形、波浪、水面波光等场...
使用requestAnimationFrame和Canvas给按钮添加绕边动画
要给按钮添加酷炫的绕边动画,可以使用Canvas来实现。基本的思路是创建一个和按钮大小相同的Canvas元素,内置在按钮元素中。然后在Canvas上实现边线环绕的动画。...
如何使用纯CSS3实现一个3D泡沫
要实现一个逼真的泡沫,涉及到比较复杂的光学/物理学知识。我们这里先简化下问题,实现一个相对简单而足够实用的泡沫元素。我们可以把基础的泡沫元素应用在很多场景中,比如水景、泡咖啡、啤酒甚至火焰特效中。泡沫首先是一个圆形元素.bubble
更多...
