核函数核技巧（Kernel Trick）白话简介

核函数是为了解决分类问题而引入的方法。

有些数据并不是那么容易线性分割，比如我们很容易用一根线条（红色）来分割下图中的黑白点：

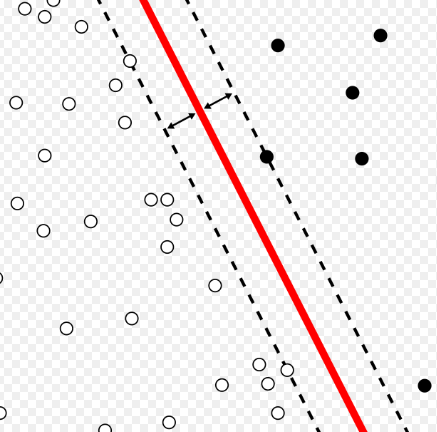
但是无法用直线来分割下图中的蓝红数据点：

为了能用简单的直线（或者多维空间的超平面）来分割如上图中的数据集，我们需要“升维”来观察和思考问题。

比如通过一定的映射，把数据映射成如下三维空间这样的分布：

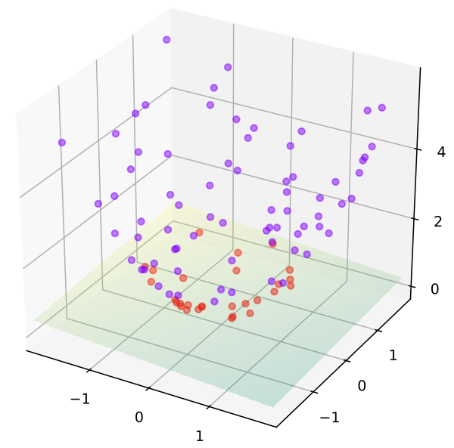
那么显然在新的维度空间中，蓝红色点可以被一个线性平面来分割。

核方法的主要思想是基于这样一个假设：

“在低维空间中不能线性分割的点集，通过转化为高维空间中的点集时，很有可能变为线性可分的”。

然而，如果直接把低维度的数据转化到高维度的空间中，然后再去寻找线性分割平面，会导致计算复杂化。

怎么解决这些问题？答案是通过核技巧（Kernel Trick）。比如原始二维空间两个点P1_ori(x1,y1)和P2_ori(x2,y2)，经过映射后变为了三维空间两个点P1(x1,y1,z1)和P2(x2,y2,z1)，接下来需要进行相似度计算（也就是计算内积<P1,P2>，内积的几何意义是一个矢量在另外一个矢量上的投影，越相近取值越大），来进一步进行分类任务。为了偷懒（避免高维度空间的内积（点积）计算），我们投机取巧的寻找出一个核函数（Kernel Function）用来简便的计算映射到高维空间之后的内积，这就是所谓的核技巧。

最后放一个人话版在线视频，帮助理解核方法的基本思想。