AI数学基础 - 如何理解傅里叶变换

傅里叶变换是信号分析的基础数学方法，其本质是把信号做分析（analysis）以及合成（synthetise），和把白光分解为彩色光谱原理类似。

傅里叶变换的基本思想是：符合一定条件下，任意周期信号可以分解为直流分量和一组不同幅值、频率、相位的正弦波。

分解的方法就是傅里叶变换。这些正弦波的频率符合一个规律：是某个频率的整数倍。这个频率，就称为基波频率，而其它频率称为谐波频率。如果谐波的频率是基波频率的N倍，就称为N次谐波。直流分量的频率为零，是基波频率的零倍，也可称零次谐波。

通过傅里叶变换，我们可以提取出一个信号的特征值（比如信号的频率组成，以及相位信息）。比如对于语音来将，可以通过低频部分获取男声，稍高频部分获取女声，而过滤掉高频噪音，对于图像（也可以当作是一种光学信号）来讲，低频部分表征物体的轮廓，而高频部分表征细节，我们人类大脑能够快速对所见所闻做傅里叶变换，从而辨识对象。

正弦函数有一个特点，叫做正交性，所谓正交性，是指任意两个不同频率的正弦波的乘积，在两者的公共周期内的积分等于零。

我们可以利用这个特性设计一个如下的检波器(下称检波器A)：

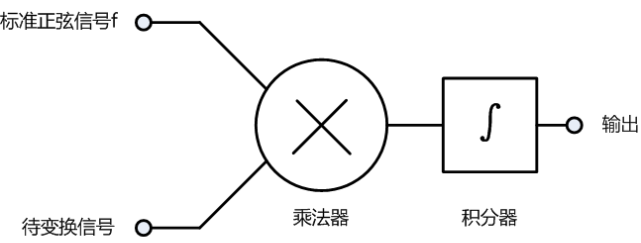
检波器A由一个乘法器和一个积分器构成，乘法器的一个输入为已知频率f的单位幅值正弦波(下称标准正弦信号f)，另一个输入为待变换的信号。检波器A的输出只与待变换信号中的频率为f的正弦分量的幅值和相位有关（其余频率分量的积分为0）。

结果非0表明有f频率分量，但结果为0并不一定表示不存在f频率分量，因为正弦波还有下述的特性：

相同频率的正弦波，当相位差为90°时(正交)，在一个周期内的乘积的积分值等于零;当相位相同时，积分值达到最大，等于两者的有效值的乘积，当相位相反时，积分值达到最小，等于两者的有效值的乘积取反。

我们知道标准正弦信号f的初始相位为零，但是，我们不知道f分量的初始相位!如果f分量与标准正弦信号f的相位刚好差90°(或270°)，检波器A输出也等于零!为此，我们再设计一个检波器B。

检波器B与检波器A的不同之处在于检波器B用一个标准余弦信号f(与标准正弦信号A相位差90°)替代滤波器A中的标准正弦信号f。如果待变换信号中包含f分量，检波器A和检波器B至少有一个输出不等于零。

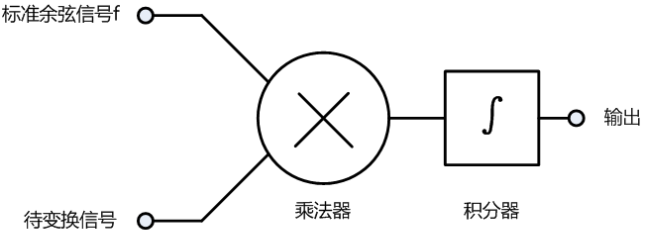
利用三角函数的基础知识可以证明，不论f分量的初始相位如何，检波器A和检波器B输出信号的幅值的方和根就等于f分量的幅值；而检波器B和检波器A的幅值的比值等于f分量初始相位的正切，如此即可求出f分量的相位。

我们再把标准正弦信号f和标准余弦信号f的频率替换成我们关心的任意频率，就可以得到输入信号的各种频率成分。如果知道输入信号的频率，把这个频率作为基波频率f，用f、2f、3f依次替代标准正弦信号f和标准余弦信号f的频率，就可以得到输入信号的基波、2次谐波和3次谐波。如此等等，就是傅里叶变换。

理解了背后的概念，我们再来看傅里叶变换公式：

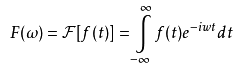
其中e^-iwt是欧拉公式cos(wt)+isin(wt)，刚好是上述的两个标准正交基，F(w)是一个复平面的向量，其模长|F(w)|非0就表示信号存在f频率分量。